Banking System 101 – Part 1

This is the first part in an ongoing series designed to guide you toward a basic understanding of Federal Reserve and ECB monetary policy as conducted in recent history, as well as what exactly constitutes and drives quantitative easing. Despite being on the forefront of the mainstream media since 2007 you will rarely run into anyone who has a thorough understanding of how all the pieces fit together. We will start with a basic introduction and  then explore a chronological recap of what has transpired in the past few years.

Fed Monetary Policy and Quantitative Easing

Before the 2008 crisis, conventional monetary policy in the US boiled down to the Federal Reserve (the Fed) controlling interest rates. The way it achieved that was by manipulating what’s known as the Fed funds rate:

Commercial banks (banks in the US that accept deposits and make loans) have daily funding requirements. Let’s assume Bank A faces a withdrawal of deposits today totaling $1bn. Deposits are a liability of the bank, so to make that payment to its customers it needs to borrow money. It could do that in the interbank market with another commercial bank, so it negotiates an overnight rate and deals at that rate.

The weighted average rate of all such transactions in the banking system every day is known as the Fed funds effective rate.  That is essentially a proxy for an overnight interbank market rate. The Fed regularly meets via Federal Open Market Committee (FOMC) and sets what is known as the Fed funds target rate, which is the level of interest rates they consider appropriate for the economy based on macroeconomic factors and so on. Their job as part of conducting monetary policy is to ensure that the market rate (ie the Fed funds effective rate) accurately mimics the benchmark Fed funds target rate.

The Fed uses Open Market Operations (OMOs) to achieve this, by directly altering the supply of money in the economy. In simple terms, think of it as two worlds: the Fed and the Monetary System (ie banks, lending institutions, and then the real economy).  The way money reaches the economy is via banks’ lending money to firms and businesses. All the money that is sitting at the Fed does not affect the economy in any way since it is not available for lending to businesses. BUT if the Fed chooses to inject money into the economy, the quantity of money that banks have available to lend increases.

Interest rate is the price of money. And similar to a stock, if supply of money increases – its ‘price’ (ie the interest rate) goes down. During Open Market Operations, the Fed buys and sells government bonds to banks as a way of regulating money supply. Suppose the Fed funds effective rate (ie the actual market rate) is trading higher than the Fed’s target (the Fed funds target rate). To lower the market rate, the Fed can attempt to increase the supply of money. To achieve this, it buys government bonds from banks, and in exchange it credits their reserve accounts. That way the money now enters the monetary system as banks can lend that money to the economy.

During Temporary OMOs, Fed reverses its actions on money supply, i.e. if it initially bought bonds from banks it will reverse that after a period of time by selling an equivalent amount, thereby creating only a temporary change in money supply. In 2009 as response to the credit crisis, the Fed announced a longer-dated programme which became the main part of their Permanent OMOs (POMOs), as they started outright purchases of longer-dated bonds without immediate intention to sell them back. This has been labelled as QE (quantitative easing).

How Does QE Work?

To illustrate, consider two US commercial banks, ie institutions that take deposits and make loans. We have Bank A, which has been started with $10bn equity capital, and has accepted $100bn of deposits. These are liabilities on its balance sheet (BS), since it effectively “owes” that money to shareholders and depositors respectively. For simplicity, consider Bank B which has exactly the same liabilities. Let’s assume for simplicity that they are the only two commercial banks in the system.

By law a bank is obliged to maintain a certain level of reserves with the central bank, which it should hold at its reserve account. This is what is known as reserve requirements and they cover the bank’s assets and liabilities but the most basic form is that banks in the US should hold 10% of their deposits as reserves. These show up as assets, since they represent cash owned by the bank.

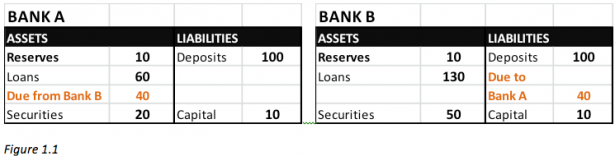
So total reserves in the system are $20bn and they are all required reserves, i.e. there are no excess reserves. Banks also make loans, which are assets on their balance sheet (since they are owed money by borrowers) and lets assume that they hold some securities on their balance sheet too (securities = stocks/bonds etc). Suppose Bank B has access to a larger pool of lending opportunities, and to be able to make more loans it has borrowed $40bn from Bank A. The full balance sheet of both banks is displayed in Figure 1.1 with the interbank loan in orange (Bank B owes money so it is a liability on its BS, and an asset on Bank A’s BS):

Note the importance of the interbank lending system in normal times, money has flown towards its most productive use (i.e. Bank B borrowed to service the need of its customers). In our example from Figure 1.1., suppose the financial system enters a period of turmoil like in 2008, which disrupted the normal pattern of lending and led to a “freeze”, which could be due to uncertainty about banks’ ability to pay back and also their ability to borrow for their own funding needs. Now Bank A does not want to continue lending to Bank B. This places a severe disruption on Bank B: if it is unable to quickly raise new deposits or borrow elsewhere to obtain the $40bn it owes, it could be forced to decrease its loans by $40bn. That in turn would force a contraction in deposits, as borrowers scramble to pay back loans to Bank B resulting in a sharp contraction in economic activity.

To prevent this, the Fed steps in with QE and suppose it buys $40bn of Treasuries from Bank B. Recall that in the original example the banking system, which consists of A and B, held no excess reserves. The resulting balance sheets after $40bn Fed QE are shown below (changes in red):

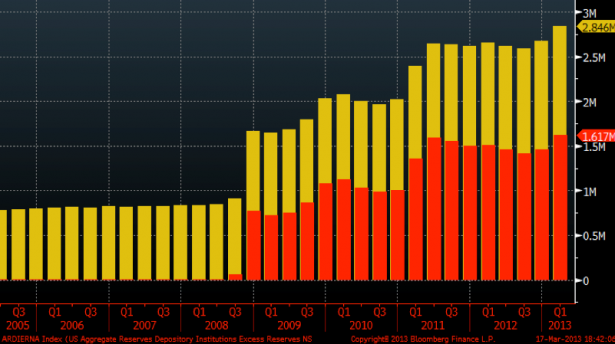
Fed credited Bank B’s reserve account with $40bn, which Bank B used to pay back the loan to Bank A (hence Bank A’s reserve account now holds extra 40bn). Bank B got the money by selling $40bn of its bonds (securities). Note that the total reserves in the system are now $60bn, but only $20bn are required – hence there are now $40bn of excess reserves. The chart below shows the actual US banking system total reserves (yellow) and excess reserves (red) that have resulted from QE, similar to the example above:

Numerous market observers and commentators such as ZeroHedge have used this to conclude that Fed has injected “dead money” that is sitting on banks’ balance sheets and hence its policies have been ineffective. But as our example shows, the job of the Fed here was to prevent an interbank market freeze and it was highly effective in this regard – it prevented Bank B from having to reduce its lending by $40bn!

In fact, lets assume that Fed does $50bn more QE, but this time the cash is released into the real economy, ie firms are sellers of the bonds to the Fed. The Fed can only deal with primary dealers which are banks, so suppose Bank B stands in as the intermediary and sells the bonds to the Fed on behalf of its clients:

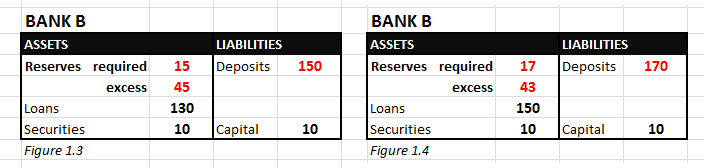
Resulting Bank B’s balance sheet is now shown in Figure 1.3 (changes in red from Figure 1.2). I have split total reserves into required and excess reserves for clarity: the Fed deals with Bank B, which is representing the firms, so it credits Bank B’s reserve account with 50bn. Bank B is selling bonds on behalf of its clients to the Fed in return, so there is no drain to Bank B’s own stockpile of securities. To channel the proceeds of this sale to its clients, Bank B must credit the deposit accounts of its clients – hence its deposits increase by $50bn from Fig 1.2. So both reserves and deposits go up, BUT required reserves are only 10% * 150bn = $15bn, hence Bank B now gains $45bn in excess reserves (it previously held none).

Let’s further assume that Bank B directly increases lending by making a new loan of $20bn to a firm. Resulting balance sheet is shown in Figure 1.4: Bank B now has a new asset (the loan to the firm of 20bn) and an offsetting liability (it credits the firm’s deposit account at the bank by 20bn). Note that Bank B’s total reserves have not changed at all, and excess reserves have only narrowed slightly to ($60bn – 10%*170bn) = $43bn.

This is counter intuitive, as even though bank lending in the economy increased, total reserves and excess reserves still went up! Sure, the firm in our example can now withdraw that money from its deposit account and spend it, but since most of the money payments are nowadays electronic whatever they spend this money on (investment, research etc) will just end up at other firms’ accounts, which in turn would end up as another bank’s deposits.

This is the general principle: loans to banks and firms and direct purchases by the central bank all increase the TOTAL level of reserves in the banking system by the same amount. It doesn’t imply anything about the level of lending in the economy! Similarly, the level of excess reserves in the system does NOT imply that banks are not lending.  In the example above bank lending went UP by nearly 10% ( = $20bn / Total loans [$150bn + $60bn] ) But Bank B’s excess reserves also went UP by $43bn.

P.L.