Banking System 101 – Part 2

This is the second part in an ongoing series designed to guide you toward a basic understanding of Federal Reserve and ECB monetary policy as conducted in recent history, as well as what exactly constitutes and drives quantitative easing. Despite being on the forefront of the mainstream media since 2007 you will rarely run into anyone who has a thorough understanding of how all the pieces fit together. We are completing our basic introduction and then will explore a chronological recap of what has transpired in the past few years. If you missed part one then please make sure you read it first before continuing below.

MONEY SUPPLY AND THE MONEY MULTIPLIER

Recall our scenario from before, with two US commercial Banks, A and B. Reserve Requirements are 10%, and the balance sheet of Bank A that we ended up with is shown below:

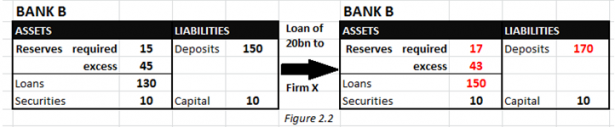
As explained before, required reserves are simply 10% of deposits, and also recall the changes to Bank B’s balance sheet after it made a loan of 20bn USD to a firm:

Changes to its BS after making a loan are highlighted in red: most importantly, excess reserves decrease slightly, as deposits grow (Bank B credits Firm X’s deposit account with the loaned money, and the loan itself appears as an asset on the BS).  Clearly this could not occur if Bank B held no excess reserves in the first place. You can think of the loan as being a case of Bank B “using up” only 2bn of its excess reserves to “create” 20bn of money in the real economy. This will become important later, as this is known as the (money) multiplier effect.

To understand this effect we need to define Money supply – simply the total quantity of monetary assets available in the economy. There are different measures of money supply, of which the important ones are:

1. Starting from the most narrow measure, we have M0 which is simply all the notes and coins in circulation. This does NOT include cash stored at the Federal Reserve Banks (ie. the central bank in the US) and cash stored at commercial banks’ vaults, as it is effectively dead money.
2. The monetary base (MB) = M0 + bank vault cash + banks’ reserve accounts. This is a broader measure, that includes notes and coins but more importantly it includes a measure of central bank money, ie required and excess reserves, which commercial banks hold at their reserve accounts with the Fed. In our example from Figure 2.1, the monetary base would equal M0 + 0 + (10+40) bn + (17+43) bn = M0 + 110bn USD.
3. M1 = M0 + demand deposits, and simply measures the money in circulation by also including the most common form of “electronic money”, which is easily accessible deposits (“on demand”), that one can use to withdraw money at any time without restrictions or delays. A common example of this is a debit (card) account.  Note that this measure does NOT include central bank money and vault cash! M1 therefore measures commercial bank money. For our example in Figure 2.1, M1 = M0 + (100bn) + (170bn) = M0 + 270bn USD [Assuming all deposits in our example are demand deposits].
4. M2 = M1 + savings accounts + “time deposits” (money has to be locked in for a period for time to earn interest, and cannot be withdrawn – e.g. bonds, money-market deposit accounts for individuals etc). This is a broader measure of commercial bank money. In our example of Figure 2.1, M2 = M1 as we assume there are only demand deposits. [ There are other broader measures of money which I will not discuss here for simplicity ]

The multiplier effect, which we described for Bank B above, can be measured in general by the money multiplier (MM) , which is simply a statistic, that measures the ratio of “commercial bank” money to “central bank” money. Out of the 4 measures of money supply listed above, only the monetary base can qualify as central bank money. So we can choose either   MM = M1/MB  or  MM = M2/MB  to be the money multiplier. Let’s take money multiplier, ie MM =  M2 / MB  as a broader measure. Firstly, let’s measure the MM for our example in Figure 2.1, substituting in our calculations for M2 and MB above:

MM = M2/MB = M1/MB = (M0 + 270bn) / (M0 + 110bn). We do not know the notes/coins in circulation (M0), but given that in modern economy it is very small compared to electronic money (ie deposits), we can assume for our example to be negligible. Therefore as M0 à 0, mathematicians reading this will know that MM à 270bn / 110bn = 2.45.

DOESN’T THE BUILD OF EXCESS RESERVES, WHICH RESULTED FROM FED QE, PREVENT THE MULTIPLIER EFFECT???

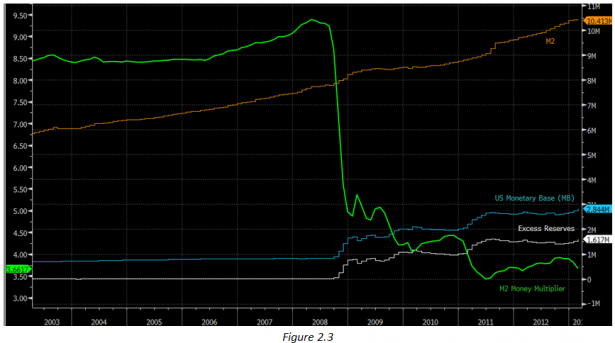
Above we can see the money supply for the US economy, and the changes that resulted since 2008: As Fed started QE, the monetary base grew, but so did excess reserves – but M2 expanded at a lower pace than before, thereby reducing the MM to ALL-TIME lows.

According to the multiplier effect, an increase in bank reserves, which resulted from QE, should have been “multiplied” into a much larger increase in M2, as banks should have expanded their deposit and lending activities. The expansion of deposits, in turn, should have raised required reserves until there are no excess reserves in the system. Why has this NOT happened in our Figure 2.3 above?

To answer this, consider the situation from a commercial bank’s perspective. Once it gains excess reserves via QE, it has two options:

1. deposit them with the Fed, in which case it would earn the Interest that the Fed pays On Excess Reserves (IOER); Since there were virtually no excess reserves until 2008, the Fed only started considering setting IOER after the 2008 crisis, and after briefly playing around with it, it was set to 0.25% and has remained that ever since.
2. attempt to lend its excess reserves to earn an interest, which is higher than IOER (0.25%).

So the bank will attempt to lend out its excess reserves at any positive interest rate, greater than IOER. This additional lending in turn decreases short-term interest rates (Why? Interest is the price of money, and if more money is supplied via lending then this price goes down).  This lending also creates additional deposits in the banking system as in Figure 2.2 and thus leads to a small increase in required reserves.  Because the increase in required reserves is small, however, the supply of excess reserves remains large. The process then repeats itself, with banks making more new loans and the short-term interest rate falling further.

This multiplier process continues until one of two things happens:

1. there are no more excess reserves, i.e. the lending has expanded so much that all excess reserves turned into required . In this case, the money multiplier is fully operational.
2. However, the process will stop before this happens if the short-term interest rate slips below what the bank can earn on its excess reserves with the Fed, i.e. IOER. At this point, there is no longer an incentive to lend and hence the multiplier process stops.

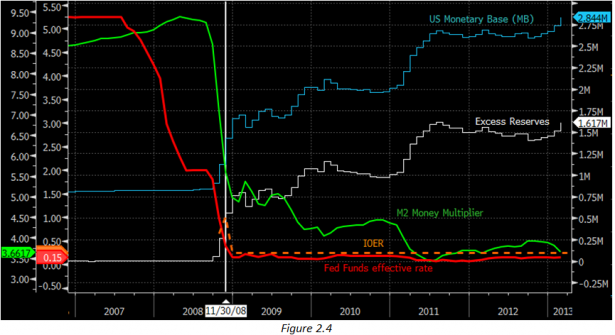
Above we add the Fed funds effective rate, currently 0.15%, (ie the actual short-term interbank lending rate), and the IOER, 0.25%, to our money supply picture from before.

Initially in 2008 the money multiplier shrunk as the credit squeeze kickstarted a massive contraction in lending (ie money supply fell), the Fed responded by aggressively cutting the Fed Funds target rate, which in turn anchored the effective rate lower. Once the FF effective rate fell below the interest Fed paid on reserves, the banks were no longer incentivised to lend and the multiplier process stopped, resulting in further collapse of the MM.

In the summer of 2012, the Fed considered cutting IOER to 0% or even negative to encourage lending but that never got much traction and another round of QE went ahead instead. I would argue on the basis of the diagram above that further rounds of QE will become increasingly less effective, and therefore cutting IOER is a much more effective next step in monetary policy.

Will excess reserves cause inflation?

The market consensus is that the large quantity of reserves will lead to an increase in the inflation rate unless the Federal Reserve acts to remove them quickly once the economy begins to recover. I would concur, as once grows picks up (IF IT PICKS UP), demand for lending will increase sharply, and the presence of such a huge amount of excess reserves, will encourage banks to lend them out aggressively – this can create an exponential surge in lending over a very short period of time, thereby resulting in runaway inflation.

However, the Fed has the power to control this via two ways:

1. Under a traditional framework, ie Fed’s Open Market Operations (OMOs), it can remove nearly all excess reserves from the banking system. It can do so by selling back Treasuries it acquired via QE: recall our review of Fed ‘s OMOs in the previous article – the primary dealers (ie banks), would have to drain their reserve accounts to put up cash in exchange for Fed’s bonds. As their reserves shrink, but clearly required reserves have stayed the same, their excess reserves therefore also diminish.
2. By raising the Interest on Excess Reserves (IOER), the Fed can manage the build-up of excess reserves more directly. As IOER is raised, it discourages banks from lending at the market rate, and instead simply park their excess reserves at the Fed. Of course, the IOER would have to be consistently set higher than the market lending rate.

The big problem here, which officials refuse to discuss, is that runaway inflation would quickly lift the market bond yields. Why? Well, imagine you are lending someone money at 5% a year, when inflation is 10%. You would be stupid, since you are effectively locking in a -5% annualized real return. Instead you could simply buy an asset, whose price grows with inflation (ie real estate) and earn 10%. Therefore, government bond yields (ie the rates at which the US Treasury borrows from the market) must also track inflation.

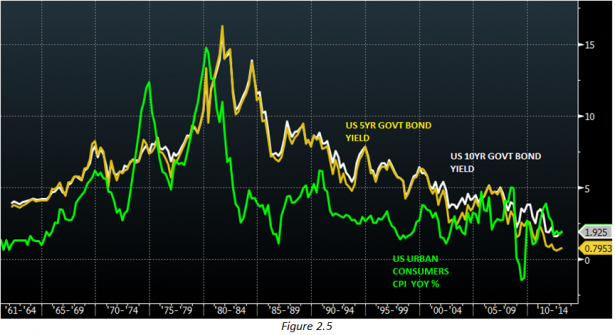
The chart above illustrates this relationship between 5yr and 10yr bond yields and CPI for the last 50 years.

So in an inflationary scenario above, the borrowing costs for the US Treasury would rise materially. If the Fed employs OMOs to combat inflation, it risks screwing with the Treasury even more, as its bond sales would also lift bond yields even further (yield is proportional to the inverse of the bond price). As the size US government debt is well publicised (including social security payments its over 500% of GDP), you can easily see that the costs of funding that debt will become unmanageable – tax receipts that the Treasury will earn from a growing economy will be nowhere near enough to pay its debt, but if it borrows more from the market it will have to commit to paying even higher interest rates in the future. This is a classic debt spiral that terminates in one of two ways:

1. Formal default. That would be the last resort, as since the US government bond market is the most liquid asset market in the world, it would bring down the Financial system globally and this time no central bank alone will be able to patch it up.
2. Pseudo-default. In this case, the Treasury would not default officially but it will effectively make the US consumer pay – by inflating away its debt. It will print an enormous quantity of USD, which will dilute the purchasing power of the consumer in real terms. This would be hugely negative for the US dollar – we are talking about a bear market of our lifetime. For historical reference, look up Weimar Germany.

Regards,

Peter Levchenko